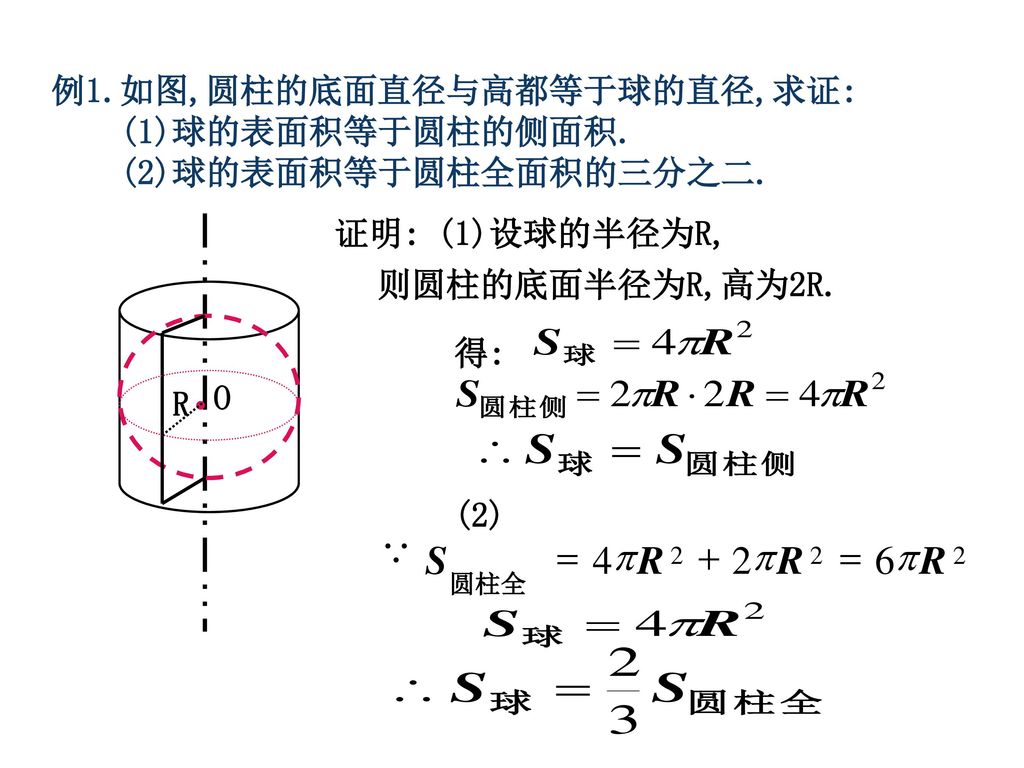
この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします. 円柱の側面積=球の表面積 を示すことによって, (円柱の側面積= なので,) 球体の表面積= を示すことができ覚えなくていい「円の面積」 算数は得意なのに数学が苦手なひとのためのブログで、 円の面積円周半径覚えなくていい「球の表面積・体積」 算数は得意なのに数学が苦手なひとのためのブログで、 球の表面積円周極間の距離 ってことをやった。どちらも底辺高さ定数の形だね。表面積の公式 「心配アール2乗」と覚える。 問題 (1) 半径 1cm の球の体積と表面積は求めなさい。 (2) 半径 2cm の球の体積と表面積は求めなさい。 (3) 半径 3cm の球の体積と表面積は求めなさい。 (4) 半径 4cm の球の体積と表面積は求めなさい。

楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ
球体面積 公式
球体面積 公式-使用目的 創作で、惑星の大きさと居住可能人口を設定するため ご意見・ご感想 漠然と、立方体の辺の長さが2倍になれば大きさが4倍になるのと同じように、球体も直径が2倍になれば表面積も4倍になるかなと思っていたが、実際に計算してみて、間違っていなかったのは少し感動した。使用目的 創作で、惑星の大きさと居住可能人口を設定するため ご意見・ご感想 漠然と、立方体の辺の長さが2倍になれば大きさが4倍になるのと同じように、球体も直径が2倍になれば表面積も4倍になるかなと思っていたが、実際に計算してみて、間違っていなかったのは少し感動した。


微分でつなげる円や球の公式 すうがくブログ 式変形ch
数学 、算数で、球について 下記2つの公式が成り立つ理由を教えてください。 球体の表面積は、球の半径をr、面積をSとすると、「S=4πr2」 球体積の公式は「V=4─3πr3」回転体の表面積も求めよう! では次,曲線をx 軸やy 軸のまわりに回転してできる回転体の曲面の表 面積を求める公式についても解説しておこう。 (Ⅰ) について,微小区間x, +Δ における 微小な曲面の表面積 ΔS は,図12 より3) 円柱面x2 y2 = a2 の円柱面x2 z2 = a2 の内部にある部分の曲面積を 求めよ。 4) xy 平面上のC1 級曲線y = f(x) (a • x • b) をx 軸のまわりに1回転 してできる曲面の曲面積は S = 2 Z b a jf(x)j p 1(f0(x))2dxとなることを証明せよ。 5) 曲面z = Arctan(y=x) (x;y > 0) の円柱面x2 y2 = a2 の内部にある部 分の曲面積を
V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin 18年夏に別チャンネルで投稿した動画に、少し編集を加えたものです。良い図があるじゃないですか。 半径r高さrの円柱の高さhでの断面積=πr^2 半径r高さrの円錐の高さhでの断面積=πh^2 半径rの球の下半分の高さhでの断面積=π(r^2h^2) (三平方の定理で確かめてください。断面は半径√r^2h^2の円です。球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半
だから、公式にも\(\displaystyle \frac{4}{3}\pi r^3\)というように3乗がある。 面積の単位には\(cm^2\)、\(m^2\)というように2乗がついているよね。 だから、公式にも\(4\pi r^2\)というように2乗がある。 このように3乗、2乗を単位と関連付けておくことで球体の表面積 球体の表面積 目標:積分を用いて上式を導出する 方法を2つ考えました. 求め方1:微笑の範囲を考える方法 求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える. 幅は 、長さは なので,表面積は3通りの方法を解説します。 積分の感覚をつかむよい練習になります。 球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です:



球缺体积和球冠表面积的计算公式及应用 晨起尘又落 Csdn博客


Http Apphy U Fukui Ac Jp Tajima Va Va17resume Pdf
①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r簡単公式三角形の面積の求め方がわかる3ステップ 中2数学 玉を取り出すときの確率を4秒で計算できる公式 中3数学 平行線と線分の比の問題の解き方がわかる3ステップ 中3数学 なぜ相似比をつかって面積比が計算できるのか?球欠 (spherical segment):球を一つの平面で切った立体 球冠 (球帽,spherical cap):球欠の側面部分 球台 (spherical segment):球を二つの平行な平面で切った立体 球帯 (spherical zone):球台の側面部分 球欠と球台は立体,球冠と球帯は曲面です。球欠は球の一部が欠けたもので,球帽は帽子


Www Spheretec Co Jp Column Pdf No16 Sphere Pdf



面積に関する質問 40ページ 勉強質問サイト
面積が (cm 2)の円の半径を求めてください。ただし円周率を 314とします。 練習問題① 半径が 2(cm)の円の面積を求めてください。ただし円周率を 314とします。 円の面積を求める公式は 円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率覚えなくていい「円の面積」 算数は得意なのに数学が苦手なひとのためのブログで、 円の面積円周半径覚えなくていい「球の表面積・体積」 算数は得意なのに数学が苦手なひとのためのブログで、 球の表面積円周極間の距離 ってことをやった。どちらも底辺高さ定数の形だね。(円の面積) = π r 2 という公式が作られる。 円の面積公式の、厳密な意味での証明は、三角関数の微分積分を待たなければならな い。しかし、この証明に出会える日本の高校生は、現行のカリキュラムでは非常に少ない。



球体体积计算公式 球体的体积 球体的体积公式 球体体积计算



球体公式 球公式 球体体积公式 球体计算公式
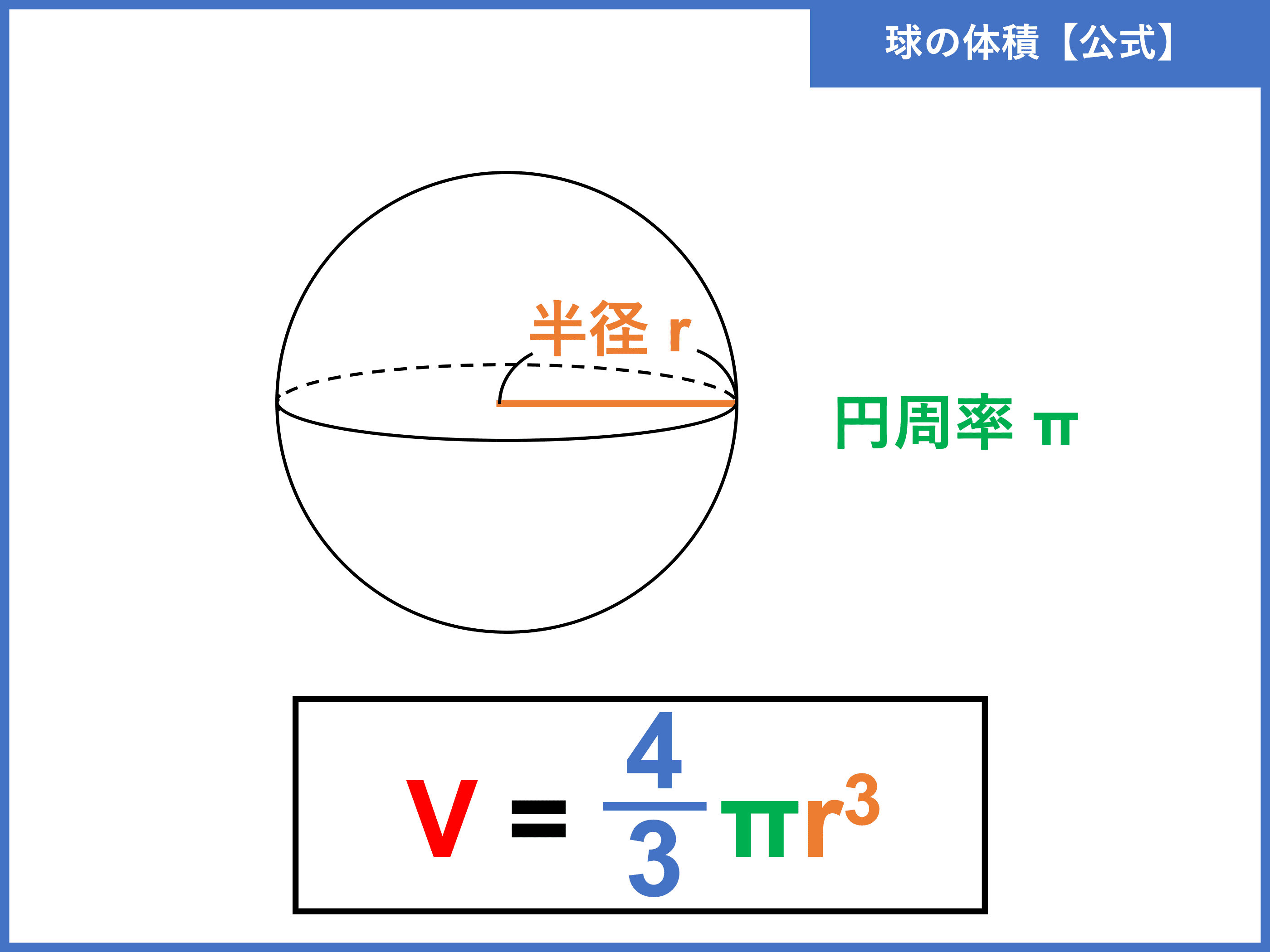
数学では「公式を丸暗記」というのはタブーに近いですが、今回はある意味しかたありません。 まずはこの公式をしっかりと覚えましょう! 公式の覚え方 それでは球体積公式を確実に覚えるためのコツを2つ紹介します。表面積の公式 「心配アール2乗」と覚える。 問題 (1) 半径 1cm の球の体積と表面積は求めなさい。 (2) 半径 2cm の球の体積と表面積は求めなさい。 (3) 半径 3cm の球の体積と表面積は求めなさい。 (4) 半径 4cm の球の体積と表面積は求めなさい。数学 、算数で、球について 下記2つの公式が成り立つ理由を教えてください。 球体の表面積は、球の半径をr、面積をSとすると、「S=4πr2」 球体積の公式は「V=4─3πr3」



球の体積と表面積 Youtube


圆柱体的表面积公式 一起来学习计算方式 爱言情
この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします. 円柱の側面積=球の表面積 を示すことによって, (円柱の側面積= なので,) 球体の表面積= を示すことができ表面積の公式 「心配アール2乗」と覚える。 問題 (1) 半径 1cm の球の体積と表面積は求めなさい。 (2) 半径 2cm の球の体積と表面積は求めなさい。 (3) 半径 3cm の球の体積と表面積は求めなさい。 (4) 半径 4cm の球の体積と表面積は求めなさい。★ 数学公式集 図形・面積・体積 For example 扇・弓・円・楕円・円錐・三角錐・角錐・球体・楕円体・台形・三角形・ など ・・


圓面積公式 圆面积计算公式 圆面积计算 半圆面积公式



すごい球体面積公式 壁紙配布
V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jinどう?球の表面積をおぼえるなんて簡単でしょ??笑 まとめ:球の表面積の求め方の公式は「ヒョウ」で覚える 球の表面積の公式はおぼえられた?? 9匹(球)のヒョウ(表面積)の捕獲に失敗(4π)したあるじ(rの二乗) という語呂さえおぼえておけ面積が (cm 2)の円の半径を求めてください。ただし円周率を 314とします。 練習問題① 半径が 2(cm)の円の面積を求めてください。ただし円周率を 314とします。 円の面積を求める公式は 円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



面積に関する質問 49ページ 勉強質問サイト
今回は、球の体積・表面積の求め方(公式)について書いていきたいと思います。 球の体積の求め方公式 球の表面積の求め方公式 球の体積・球の表面積を求める問題 問題① 《球の体積の求め方》 《球の表面積の求め方》 問題② 《球の体積の求め方》 《球の表面積の求め方》 問題簡単公式三角形の面積の求め方がわかる3ステップ 中2数学 玉を取り出すときの確率を4秒で計算できる公式 中3数学 平行線と線分の比の問題の解き方がわかる3ステップ 中3数学 なぜ相似比をつかって面積比が計算できるのか?前述の通り、球体の表面積 v を求める公式は、次の通りです。 \begin{align*} V = 4 \pi r^2 \end{align*} この式に出てくる文字の意味は、次の通りです。



円と球 3つの公式その由来 山口自然情報 わくわくどきどきサイエンス 別館



ジオドーム4 Nv The North Face ザ ノース フェイス 公式通販


半圆体积公式 半圆的体积 圆体积公式 圓面積公式



18 号 電磁波吸収及び輻射材料及びその製造方法並びに赤外線源 Astamuse


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



高校数学b 2つの球面の交線と交線を含む平面の方程式 球面束 受験の月


神戸ノート b5 算数帳 小学校3 4年用 Sansuu34 Art Bungu In Kobe 通販 Yahoo ショッピング



カセット 自転車 テレックス Laq ビックカメラ Hisamichi Jp



中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



小6 算数 小6 2 円の面積 応用編 Youtube



球公式 双色球公式 球体公式 双色球公式算法



球と立体角 Yoshihiraのスペース



Vpetiysk6hw2tm


披薩定理 维基百科 自由的百科全书



円の面積 球の体積公式の証明 理系ノート



Amazon Co Jp 19 Avp Austin Open 2日目 Generic



椭球体的体积 椭球体积计算公式 椭圆球体积公式 椭球体的体积计算公式



高校数学 楕円の面積と回転体の体積 受験の月



すごい球体面積公式 壁紙配布



立體角 维基百科 自由的百科全书
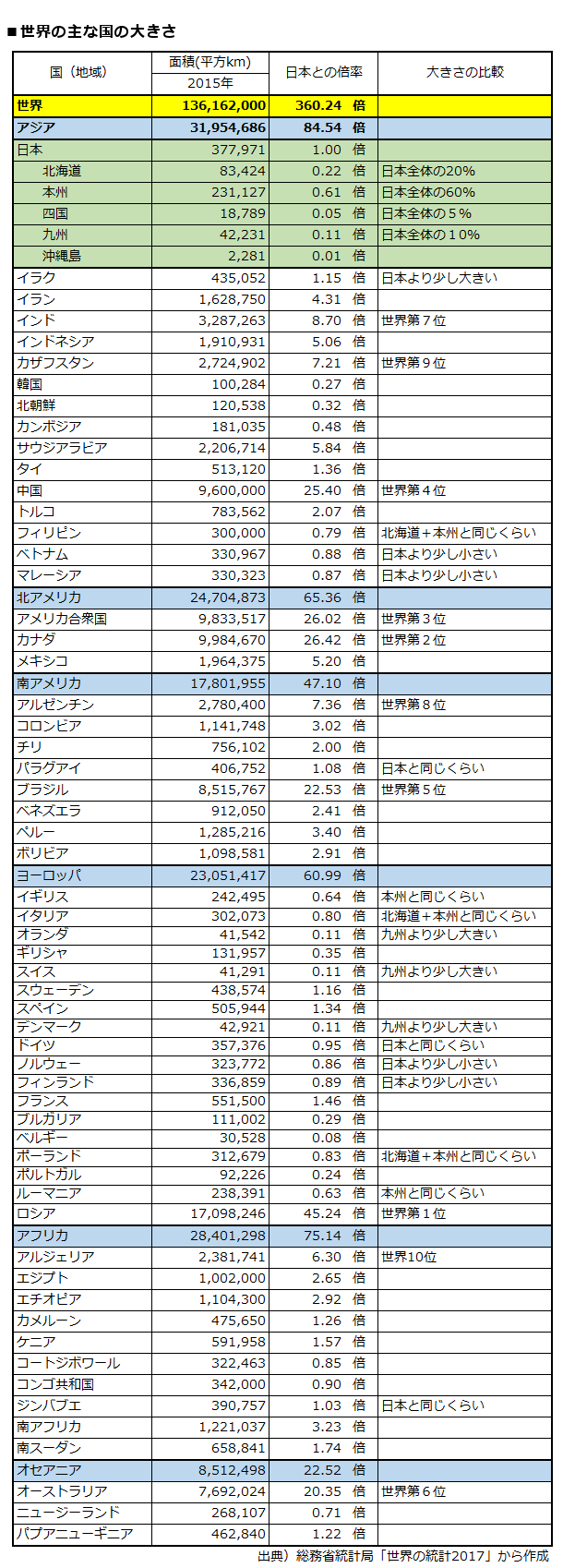


実際の面積に合わせて修正された世界地図 ヨーロッパは意外に小さい ウサコッツ飼育日記



楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ



球の体積公式の微分が表面積になっている理由 Youtube


62章 流れの中の球体の抗力



楽天市場 ふるさと納税 久留米絣トートバック ボール ティセット Im 日本三大絣 久留米絣 トートバッグ 手提げ バッグ ゴルフボール ティセット シンプル カジュアル 送料無料 福岡県久留米市



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ


Http Www Kurims Kyoto U Ac Jp Kyodo Kokyuroku Contents Pdf 1392 8 Pdf



カセット 自転車 テレックス Laq ビックカメラ Hisamichi Jp



青チャート 例題240 3次曲線と面積 高校数学に関する質問 勉強質問サイト
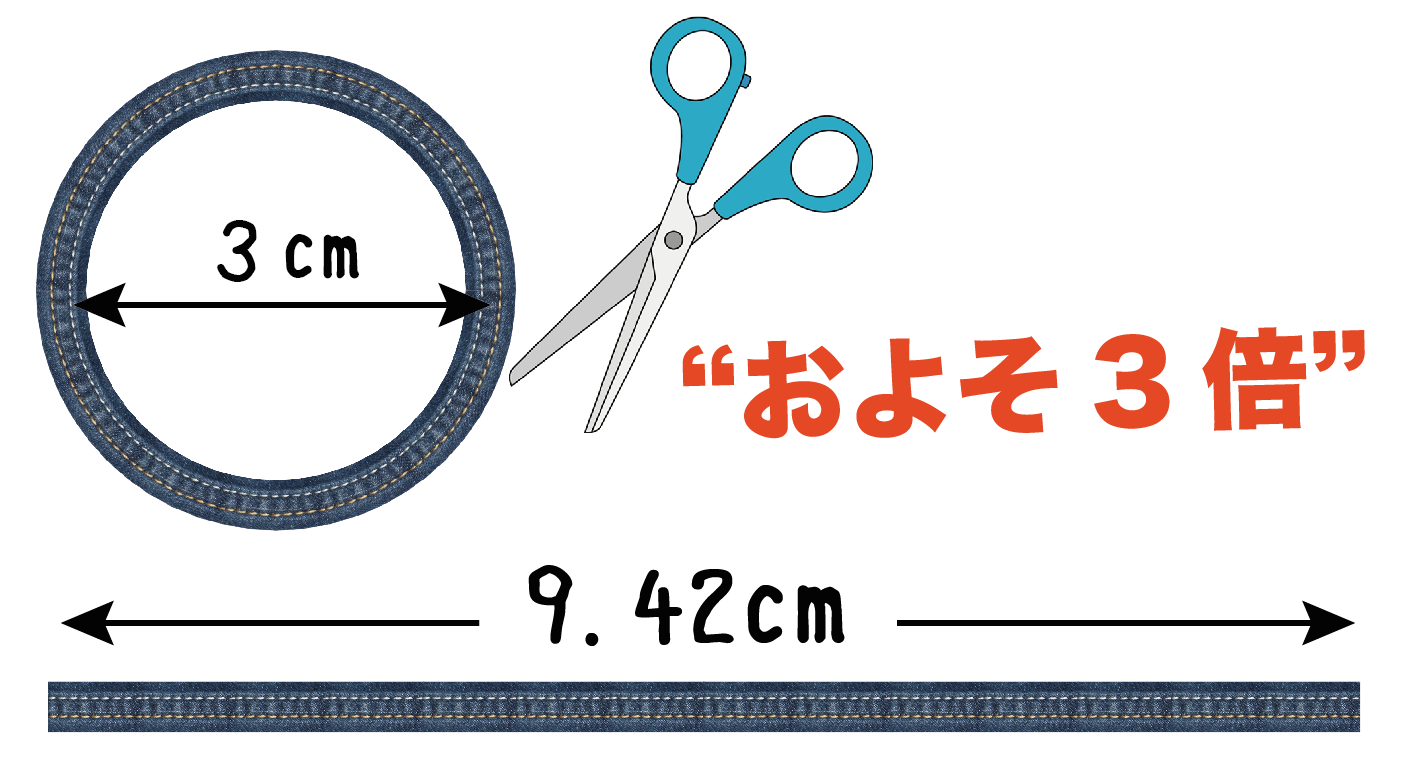


直径から計算 円周の長さの求め方 の公式を3秒で覚える方法 Qikeru 学びを楽しくわかりやすく



おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



球面上の三角形の面積公式が美しすぎる 証明はもっと美しい Youtube



Wkq J3t Omv M



球の表面積を重積分を使って計算してみた Youtube



微分でつなげる円や球の公式 すうがくブログ 式変形ch


Http Www Ms U Tokyo Ac Jp Tambara Docs C4jh08 1tsuboi Pdf



円 断 面積 公式



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



面積に関する質問に関する質問 65ページ 勉強質問サイト



球と円柱について Wikipedia


球的表面积体积公式 球面积计算公式 球的面积公式 球的表面积计算公式
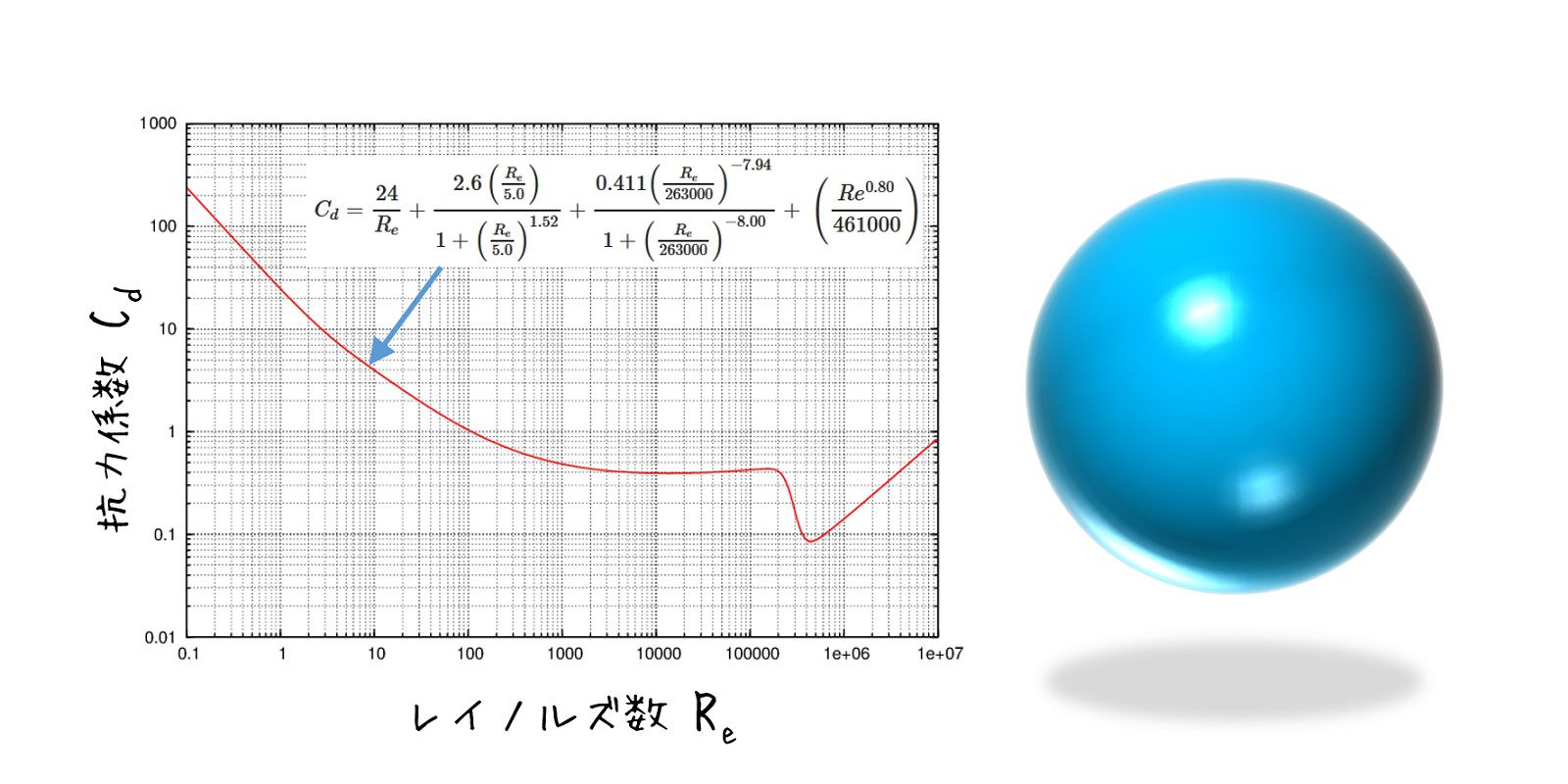


球体の空気抵抗と係数 シキノート



球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube



すごい球体面積公式 壁紙配布



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



運動エネルギーまとめ 公式 単位 求め方 位置エネルギーとの関係 理系ラボ



すごい球体面積公式 壁紙配布



ピクサーの作品は 想像力と技術の融合から生まれる トイ ストーリー に携わり続けた小西園子さんが夢見る アニメーションの未来とは
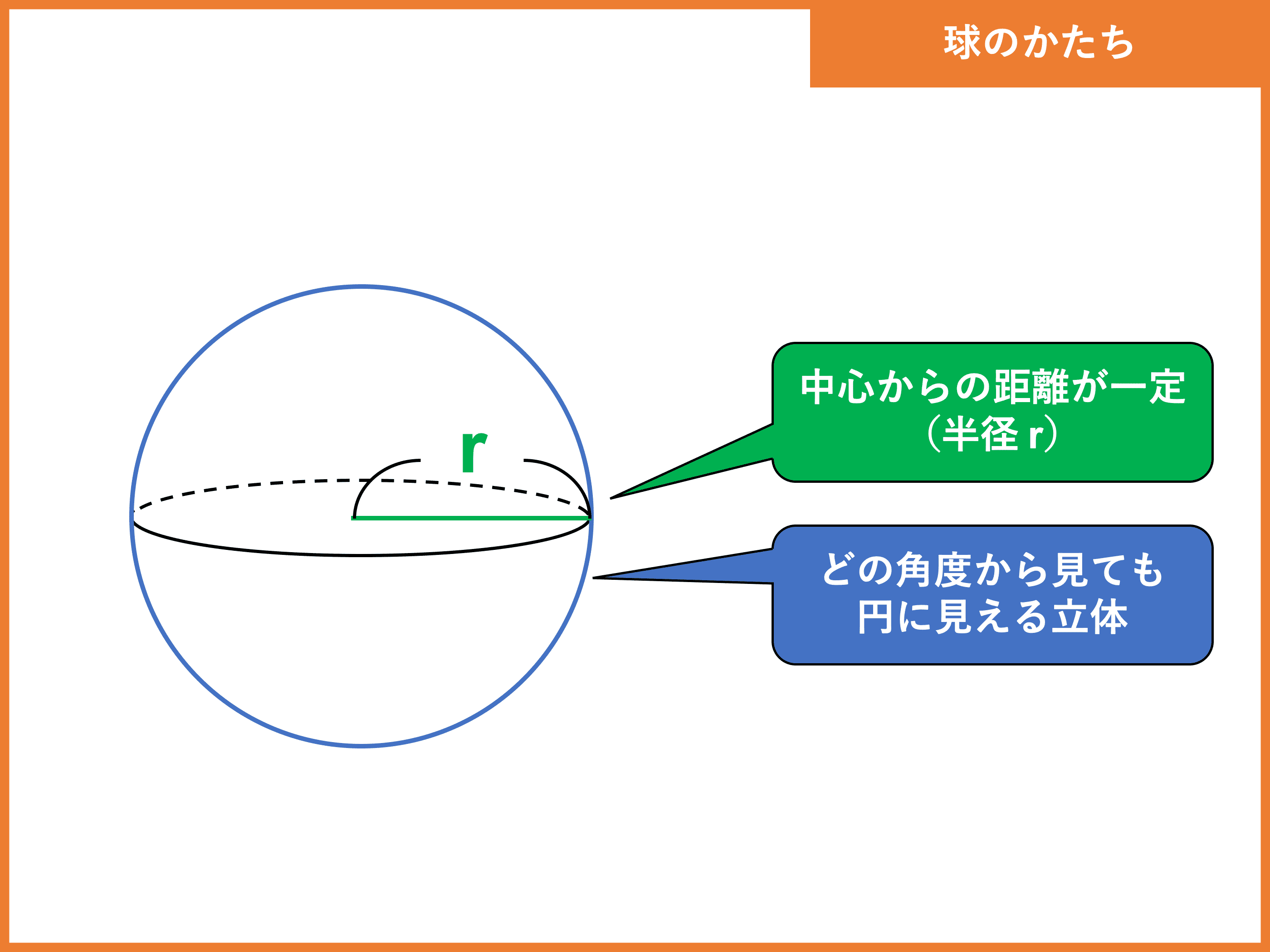


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



青チャート 例題240 3次曲線と面積 高校数学に関する質問 勉強質問サイト



高校数学b 空間の球面と平面の交線 受験の月
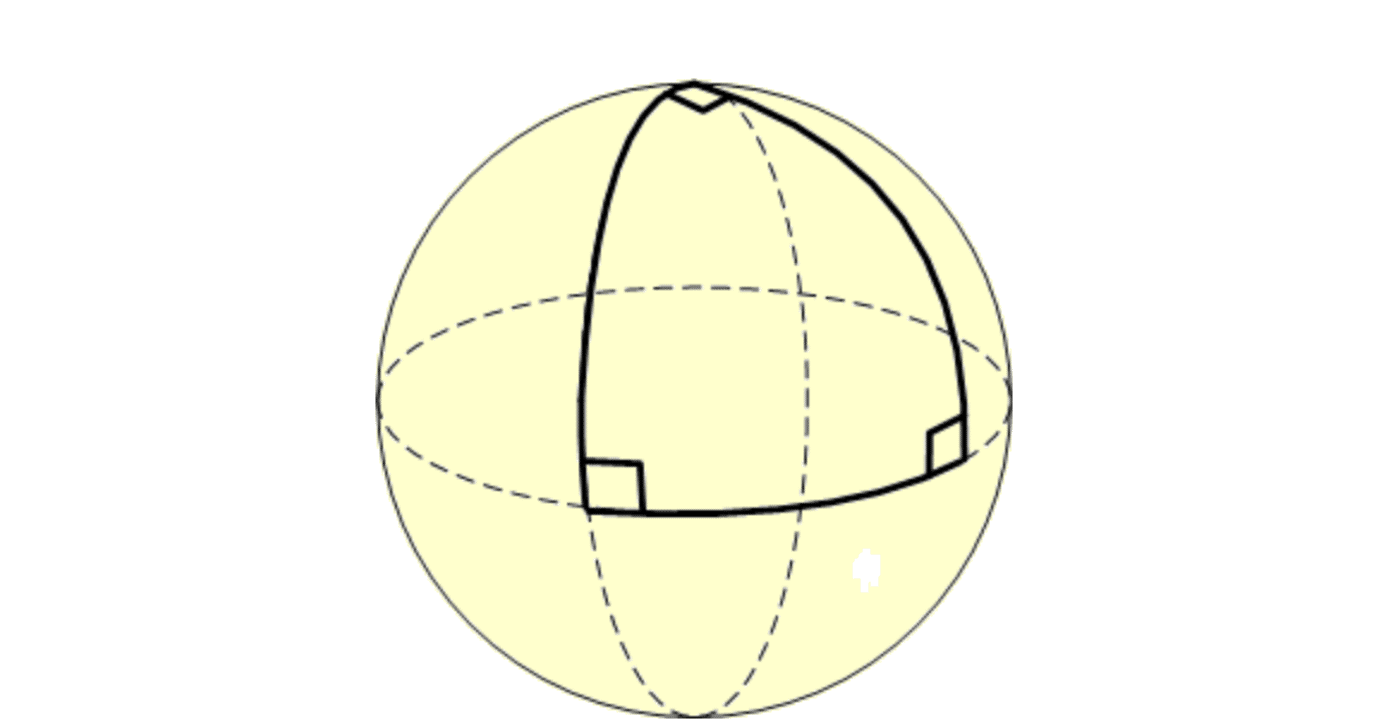


オイラーの公式とトポロジー Sgk Note



高校数学 正四面体の計量 表面積 2面のなす角 高さ 体積 内接球の半径 外接球の半径と立方体への埋め込み 受験の月



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



10岁郭承曦用英文开讲 证明球体体积公式的八种方法 Youtube



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



最高のコレクション扇面積公式 リタ ベルナル



数学だって実験するんです 実験で球の面積公式を覚えよう 艇学
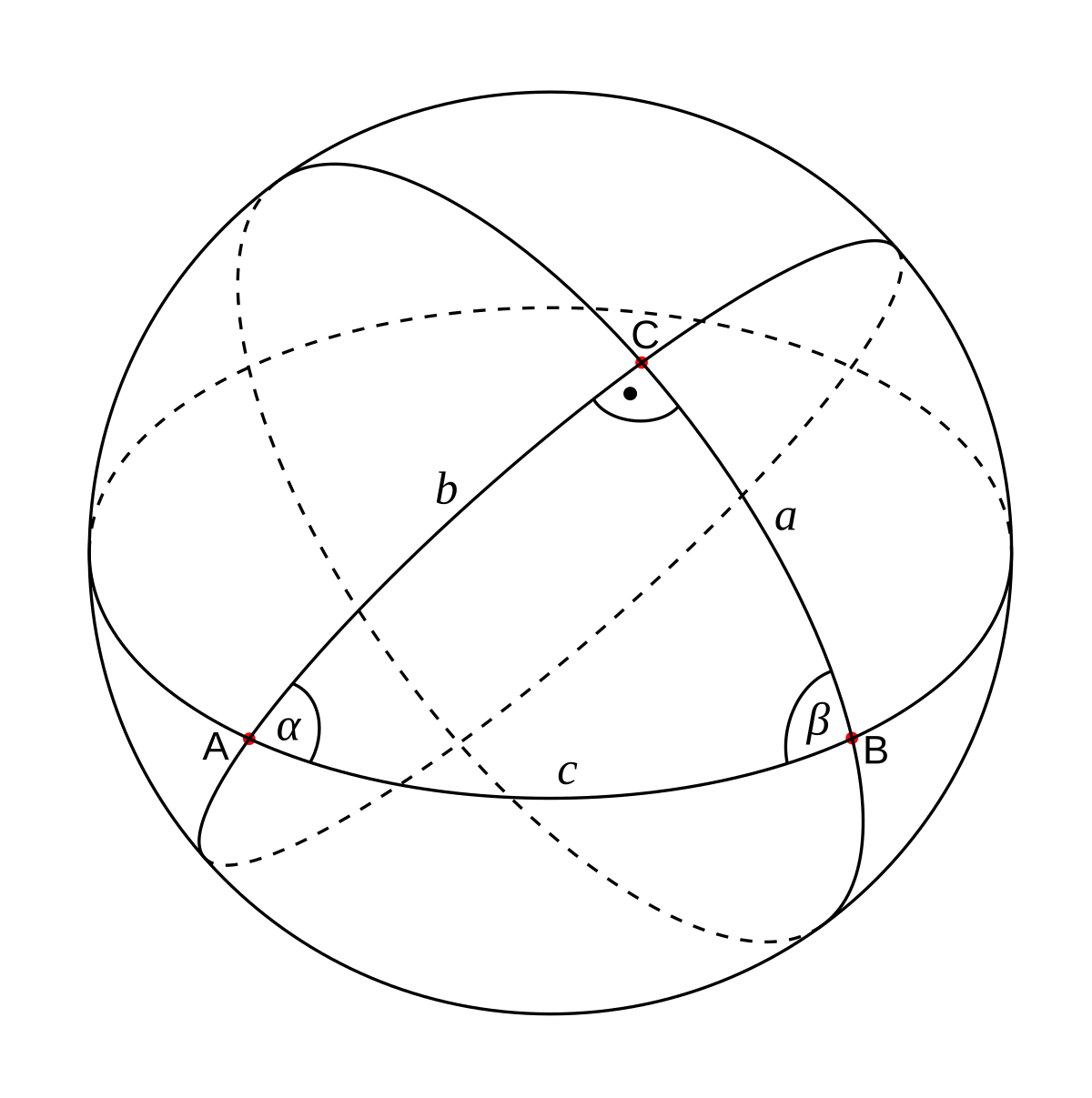


球面三角法 Wikipedia



簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく



最高 50 正三角形 面積 求め方


ブラジル Wikipedia



4种方法来求四边形的面积



正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ



アートアクアリウム美術館が年8月にオープン決定 アートアクアリウム公式サイト
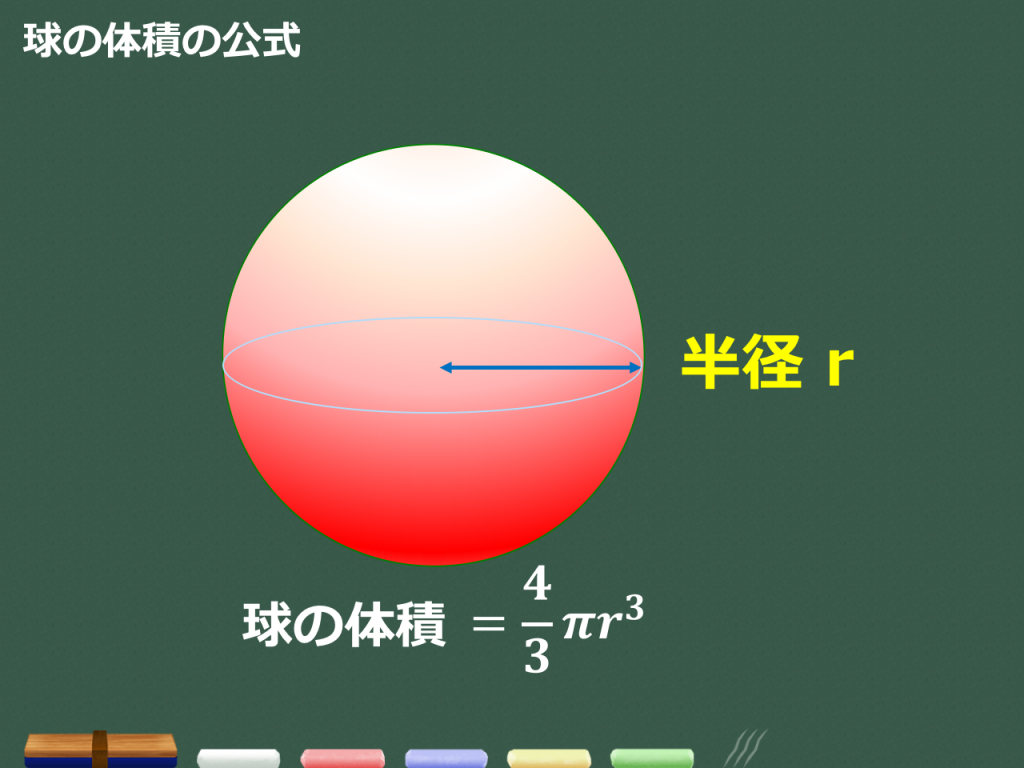


3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ



中1 数学 中1 84 球について Youtube



新しい 球体 体積 求め 方 壁紙 配布



面積及體積 Dse Maths Helper



面白数学 球の表面積 円の面積 4の理由 東大生の高校数学ブログ



Hypersphere ハイパースフィア 振動式ボールで局部的なアプローチが可能 Hyperice日本公式サイト



中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト



球公式 双色球公式 球体公式 双色球公式算法



曲面積の求め方 Notes Jp



優雅 球体 表面積 求め 方 壁紙 配布



公式店舗 こいのぼり キング印 鯉のぼり 庭園用 8m8点 ナイロン鯉 祥龍吹流し 家紋 名前入れ可能 年度新作 Ym 人形屋ホンポ特急 雛人形五月人形 Silaciems Lv


モルテン バスケットボール 6号球 公式球 Bgl6 一般女子 大学女子 高校女子 中学校用 Bg6l Aksports 通販 Yahoo ショッピング



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



すごい球体面積公式 壁紙配布



アートアクアリウム美術館 東京 日本橋に誕生 過去最大30 000匹超の金魚が泳ぐアート空間 ファッションプレス



中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
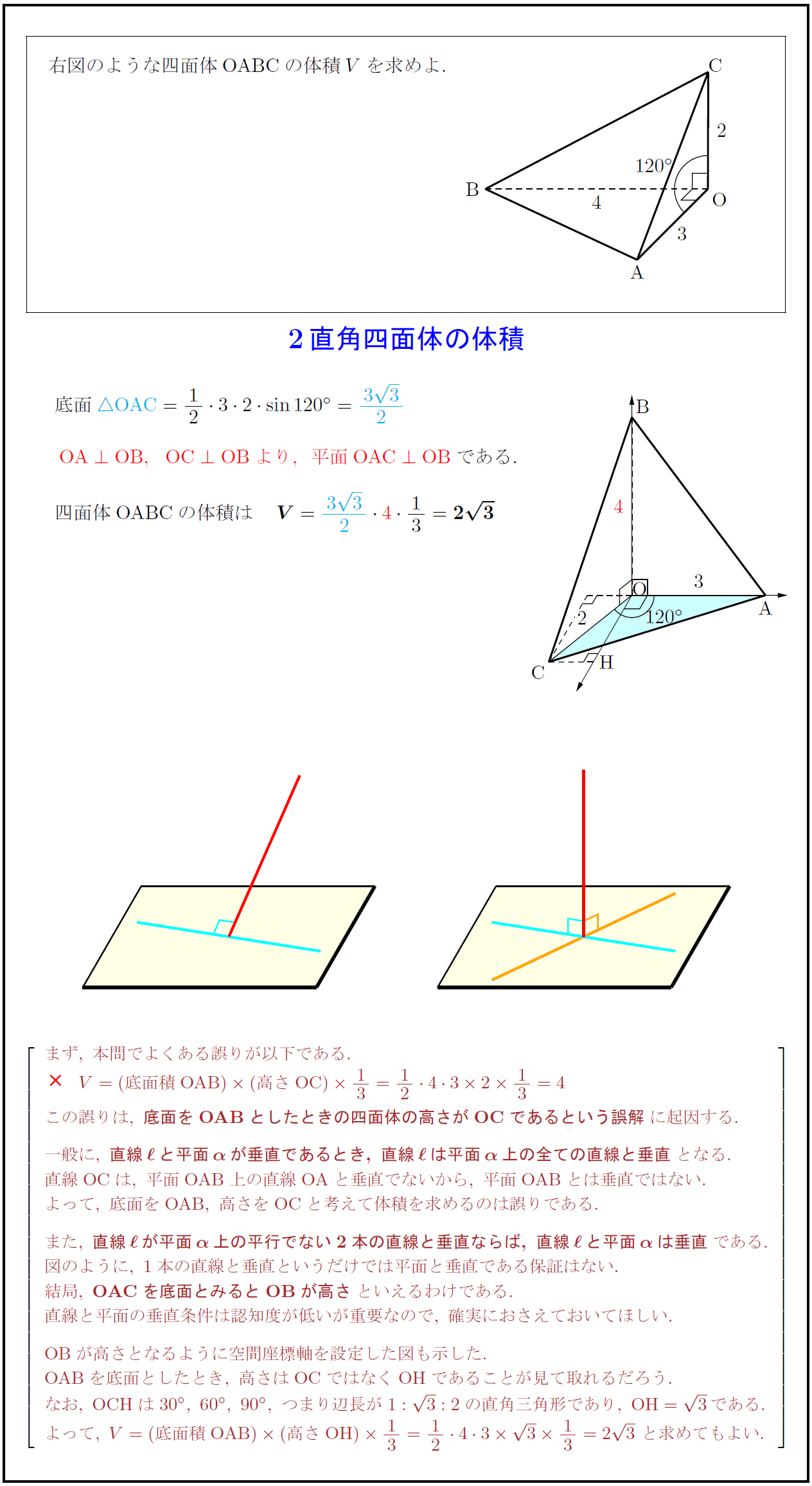


高校数学 2直角四面体の体積 直線と平面の垂直条件 受験の月



高校数学b 空間の球の接平面の方程式 X X Y Y Z Z R 受験の月



数学 積分の面積が2等分 高校数学に関する質問 勉強質問サイト



青チャート 例題240 3次曲線と面積 高校数学に関する質問 勉強質問サイト


すごい球体面積公式 壁紙配布



0 件のコメント:
コメントを投稿